import SCOTCH
import pandas as pd
import anndata as ad
import scanpy as sc
import torch
import matplotlib.pyplot as plt
Running SCOTCH on Simulated Data¶
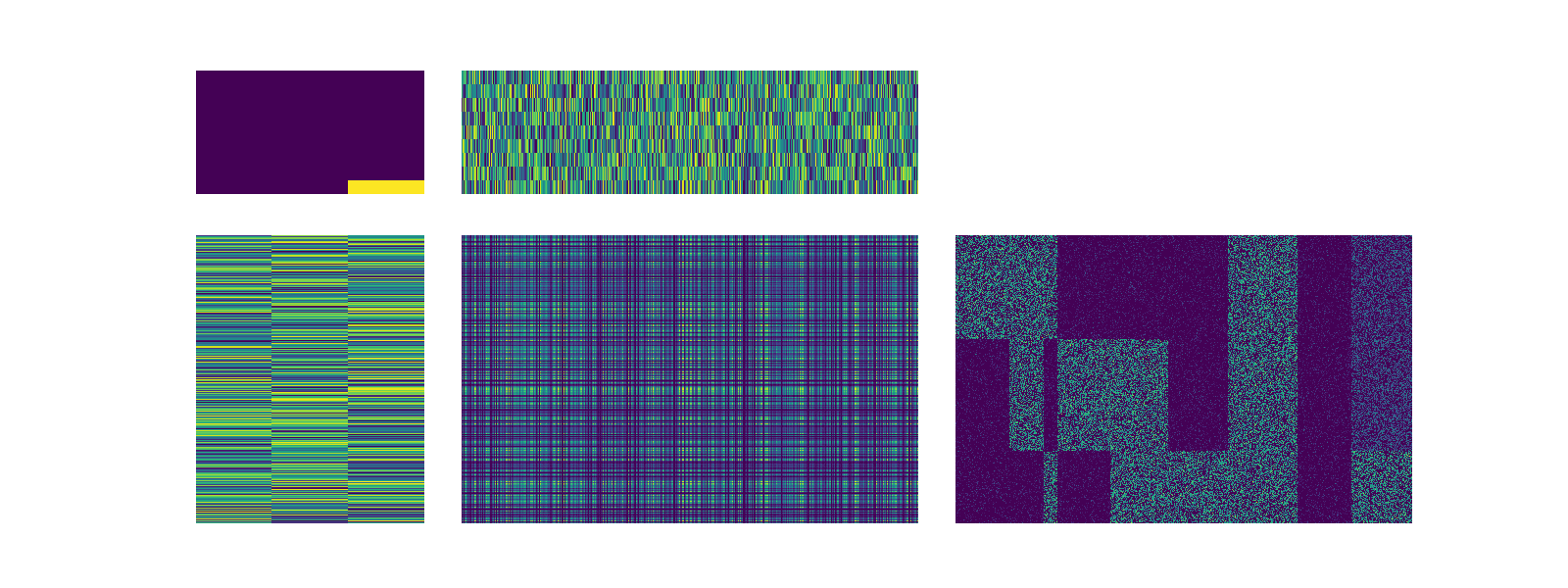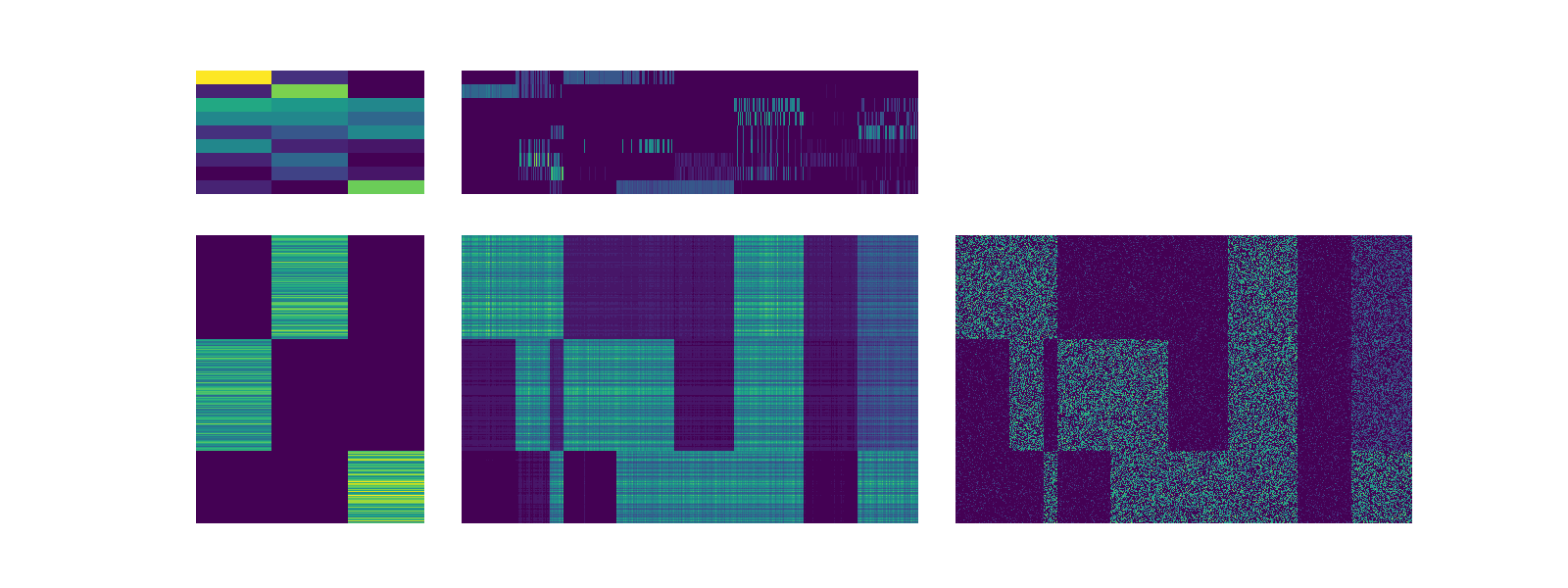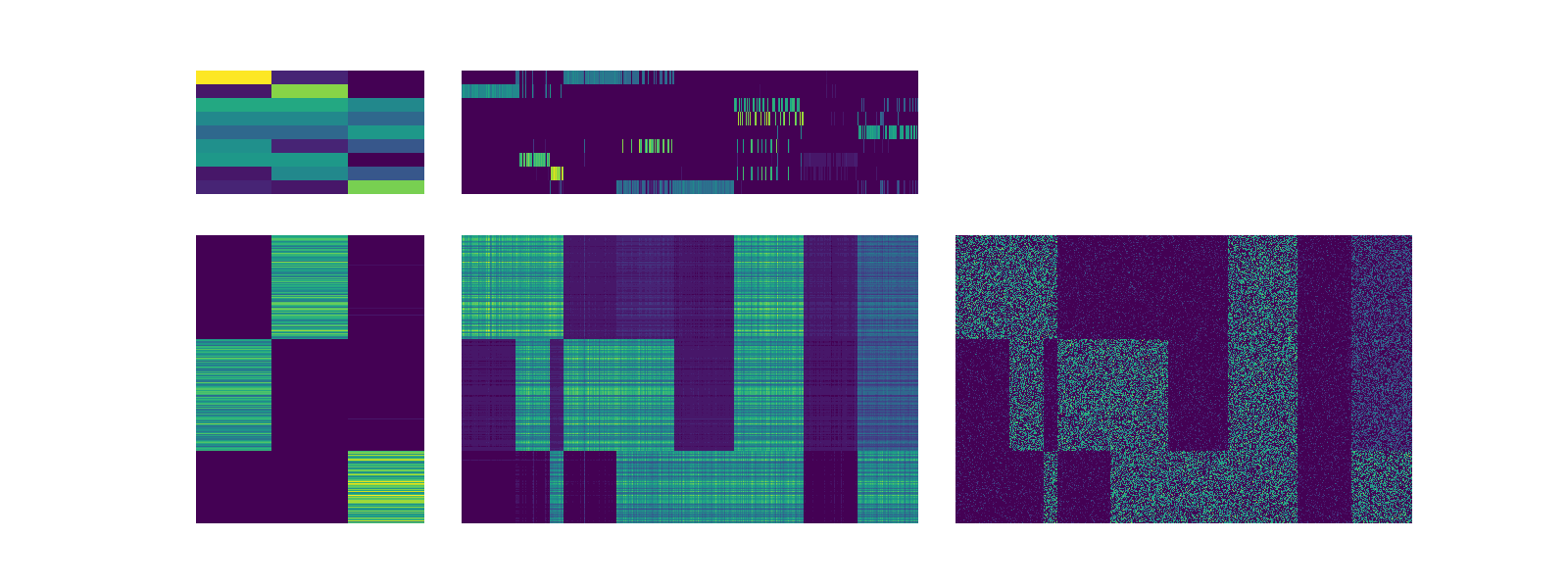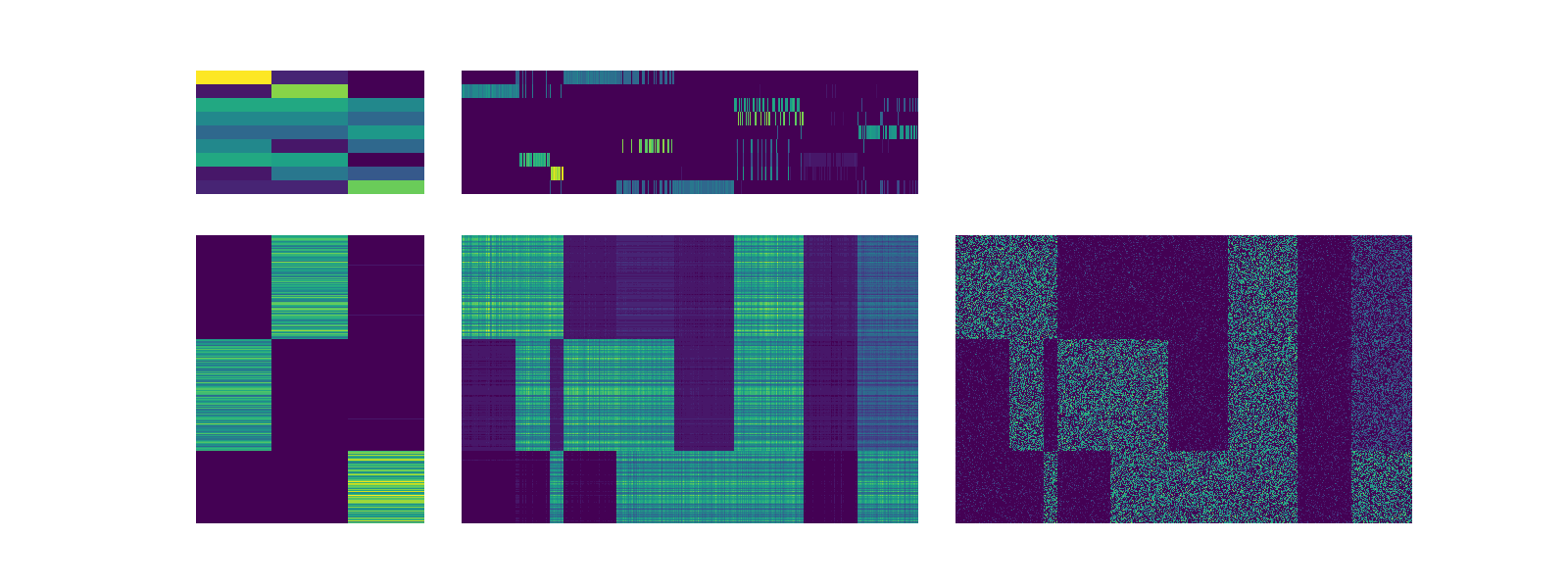
This notebook is an example of utilizing SCOTCH to factor an example matrix, with a generated block structure. The matrix is found in the text "test/A.txt". The matrix contains 500 rows and 1000 columns. The matrix naturally can be factorized into 3 row clusters and 9 column clusters. In the code block below, we load the A matrix into a pandas dataframe and visualize the heatmap.
A = pd.read_csv("test/A.txt", sep = '\t', header=None)
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot()
ax.imshow(A, cmap='viridis', interpolation='nearest')
ax.set_axis_off()
SCOTCH interfaces with anndata structure to perform its . In the next code block we convert A into an anndata object and initialize a scotch object. For the first factor example, we are using $k1=3$, and $k2 = 9$. These are the expected number of row and column clusters respectively. $max\_l\_u$ and $max\_l\_v$ corresponds to the orthogonal regularization parameter. In general, it is recommended to use regularization with scotch. We are running it without regularization in the context to demonstrate the poor clustering performance and to estimate the error associated NMTF without regularization.
An explanation of the remaining parameters is below:
var_lambda: SCOTCH allows for a ramping of the regularization parameters using a sigmoid scheduler. In general this is not need to determine good clusters and embeddings. By setting this to False, the max_l_u and max_l_v values are used for all interactions of the update.
device: SCOTCH updates are GPU enabled for reasonably sized feature matrices. If using a GPU this should point to the name of the GPU device.
init_style: SCOTCH supports multiple different NM(T)F initializations. Here we are initializing all elements of $U$, $V$, and $S$. Other supported values of this parameter are "nnsvd" for non-negative SVD initialization.
draw_intermediate_graph: This parameter allows for visualization of the factors and estimates during the SCOTCH update. Each full update of $U$, $S$, and $V$ are captured into a frame and stitched together and can be stitched into a GIF. Including this parameter does slow down the update especially for large expression matrices.
After initializing SCOTCH, we add the data from adata object to scotch for factorization.
adata = ad.AnnData(A)
scotch = SCOTCH.SCOTCH(k1 = 3, k2 = 9, max_l_u = 0.0, max_l_v = 0.0, term_tol = 1e-10, var_lambda= False, device = "cpu", init_style="random", draw_intermediate_graph=True)
scotch.add_data_from_adata(adata)
/opt/anaconda3/envs/Pytorch/lib/python3.9/site-packages/anndata/_core/aligned_df.py:67: ImplicitModificationWarning: Transforming to str index.
warnings.warn("Transforming to str index.", ImplicitModificationWarning)
/opt/anaconda3/envs/Pytorch/lib/python3.9/site-packages/anndata/_core/aligned_df.py:67: ImplicitModificationWarning: Transforming to str index.
warnings.warn("Transforming to str index.", ImplicitModificationWarning)
This block runs SCOTCH. If the verbose SCOTCH input parameter The following information is printed for each iteration:
- Iter - the current interation that is being run.
- Iter time - The time that it took to complete the iteration. Iteration 1 generally takes longer than all other iters due to some initialization at the beginning of SCOTCH.
- Total time - the current run time.
- Objective - An estimate of the objective.
- Relative Delta Objective - The change relative in the objective from the previous iteration. When this value is less that term_tol, and greater than zero the algorithm with stop.
- Reconstruction error - This is the component of the objective related to $|| X - USV^T ||_F^2$. This value is comparable across different random initialization or with different regularization parameters.
scotch.fit()
Initializing NMTF factors Beginning NMTF Iter: 1 Iter Time: 0.241 Total Time: 0.241 Objective: 8.195e+06 Relative Delta Objective: 2.086e-01 Reconstruction Error: 8.195e+06 Iter: 2 Iter Time: 0.061 Total Time: 0.302 Objective: 8.021e+06 Relative Delta Objective: 2.124e-02 Reconstruction Error: 8.021e+06 Iter: 3 Iter Time: 0.058 Total Time: 0.360 Objective: 7.722e+06 Relative Delta Objective: 3.729e-02 Reconstruction Error: 7.722e+06 Iter: 4 Iter Time: 0.051 Total Time: 0.411 Objective: 7.339e+06 Relative Delta Objective: 4.962e-02 Reconstruction Error: 7.339e+06 Iter: 5 Iter Time: 0.056 Total Time: 0.467 Objective: 7.143e+06 Relative Delta Objective: 2.665e-02 Reconstruction Error: 7.143e+06 Iter: 6 Iter Time: 0.055 Total Time: 0.522 Objective: 6.968e+06 Relative Delta Objective: 2.456e-02 Reconstruction Error: 6.968e+06 Iter: 7 Iter Time: 0.057 Total Time: 0.579 Objective: 6.861e+06 Relative Delta Objective: 1.528e-02 Reconstruction Error: 6.861e+06 Iter: 8 Iter Time: 0.136 Total Time: 0.715 Objective: 6.824e+06 Relative Delta Objective: 5.451e-03 Reconstruction Error: 6.824e+06 Iter: 9 Iter Time: 0.054 Total Time: 0.768 Objective: 6.812e+06 Relative Delta Objective: 1.791e-03 Reconstruction Error: 6.812e+06 Iter: 10 Iter Time: 0.048 Total Time: 0.817 Objective: 6.807e+06 Relative Delta Objective: 6.477e-04 Reconstruction Error: 6.807e+06 Iter: 11 Iter Time: 0.046 Total Time: 0.863 Objective: 6.806e+06 Relative Delta Objective: 2.322e-04 Reconstruction Error: 6.806e+06 Iter: 12 Iter Time: 0.044 Total Time: 0.907 Objective: 6.805e+06 Relative Delta Objective: 9.426e-05 Reconstruction Error: 6.805e+06 Iter: 13 Iter Time: 0.054 Total Time: 0.961 Objective: 6.805e+06 Relative Delta Objective: 4.372e-05 Reconstruction Error: 6.805e+06 Iter: 14 Iter Time: 0.047 Total Time: 1.008 Objective: 6.804e+06 Relative Delta Objective: 2.271e-05 Reconstruction Error: 6.804e+06 Iter: 15 Iter Time: 0.041 Total Time: 1.049 Objective: 6.804e+06 Relative Delta Objective: 1.279e-05 Reconstruction Error: 6.804e+06 Iter: 16 Iter Time: 0.044 Total Time: 1.092 Objective: 6.804e+06 Relative Delta Objective: 7.495e-06 Reconstruction Error: 6.804e+06 Iter: 17 Iter Time: 0.047 Total Time: 1.140 Objective: 6.804e+06 Relative Delta Objective: 4.556e-06 Reconstruction Error: 6.804e+06 Iter: 18 Iter Time: 0.043 Total Time: 1.183 Objective: 6.804e+06 Relative Delta Objective: 2.719e-06 Reconstruction Error: 6.804e+06 Iter: 19 Iter Time: 0.042 Total Time: 1.224 Objective: 6.804e+06 Relative Delta Objective: 1.690e-06 Reconstruction Error: 6.804e+06 Iter: 20 Iter Time: 0.046 Total Time: 1.271 Objective: 6.804e+06 Relative Delta Objective: 1.029e-06 Reconstruction Error: 6.804e+06 Iter: 21 Iter Time: 0.044 Total Time: 1.314 Objective: 6.804e+06 Relative Delta Objective: 6.614e-07 Reconstruction Error: 6.804e+06 Iter: 22 Iter Time: 0.133 Total Time: 1.447 Objective: 6.804e+06 Relative Delta Objective: 3.674e-07 Reconstruction Error: 6.804e+06 Iter: 23 Iter Time: 0.043 Total Time: 1.491 Objective: 6.804e+06 Relative Delta Objective: 2.205e-07 Reconstruction Error: 6.804e+06 Iter: 24 Iter Time: 0.043 Total Time: 1.534 Objective: 6.804e+06 Relative Delta Objective: 1.470e-07 Reconstruction Error: 6.804e+06 Iter: 25 Iter Time: 0.044 Total Time: 1.578 Objective: 6.804e+06 Relative Delta Objective: 1.470e-07 Reconstruction Error: 6.804e+06 Iter: 26 Iter Time: 0.042 Total Time: 1.620 Objective: 6.804e+06 Relative Delta Objective: 0.000e+00 Reconstruction Error: 6.804e+06
If the draw_intermediate_graph is set to true, you can write a gif using the following function after initialization. It is saved to the SCOTCH output directory, under the following file name.
scotch.write_gif('NMTF_no_reg.gif')
writing gif to ./NMTF_no_reg.gif
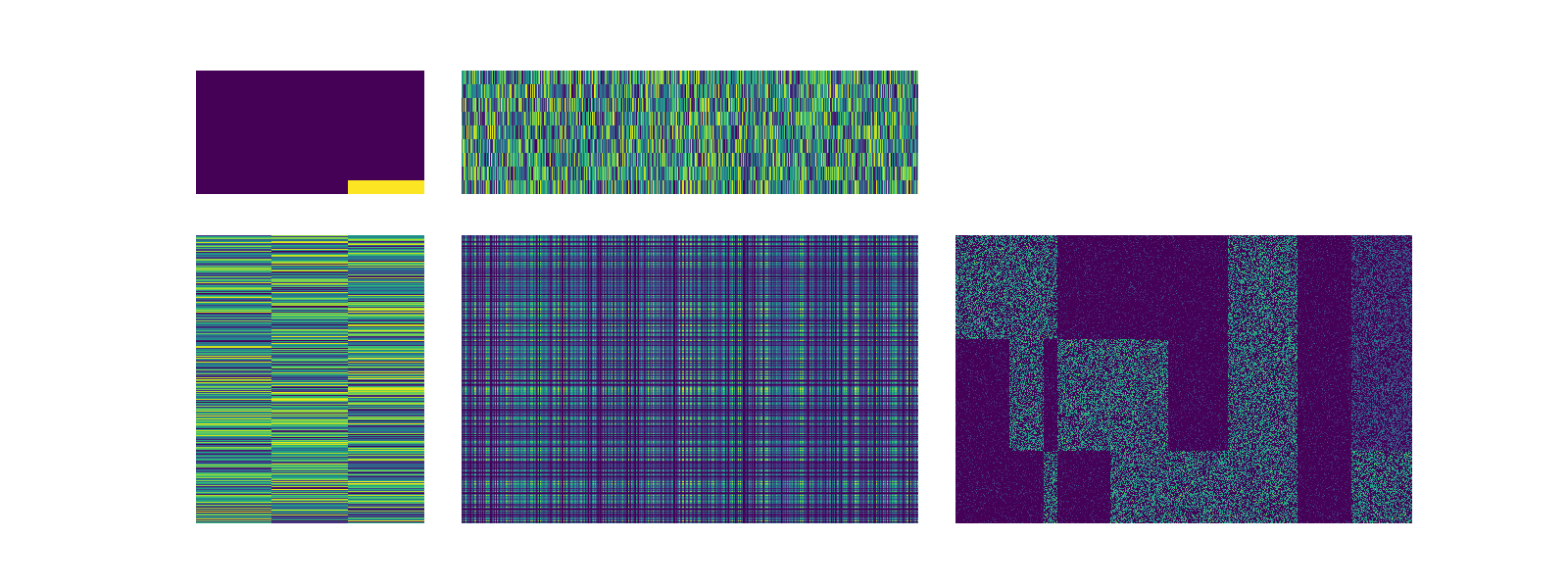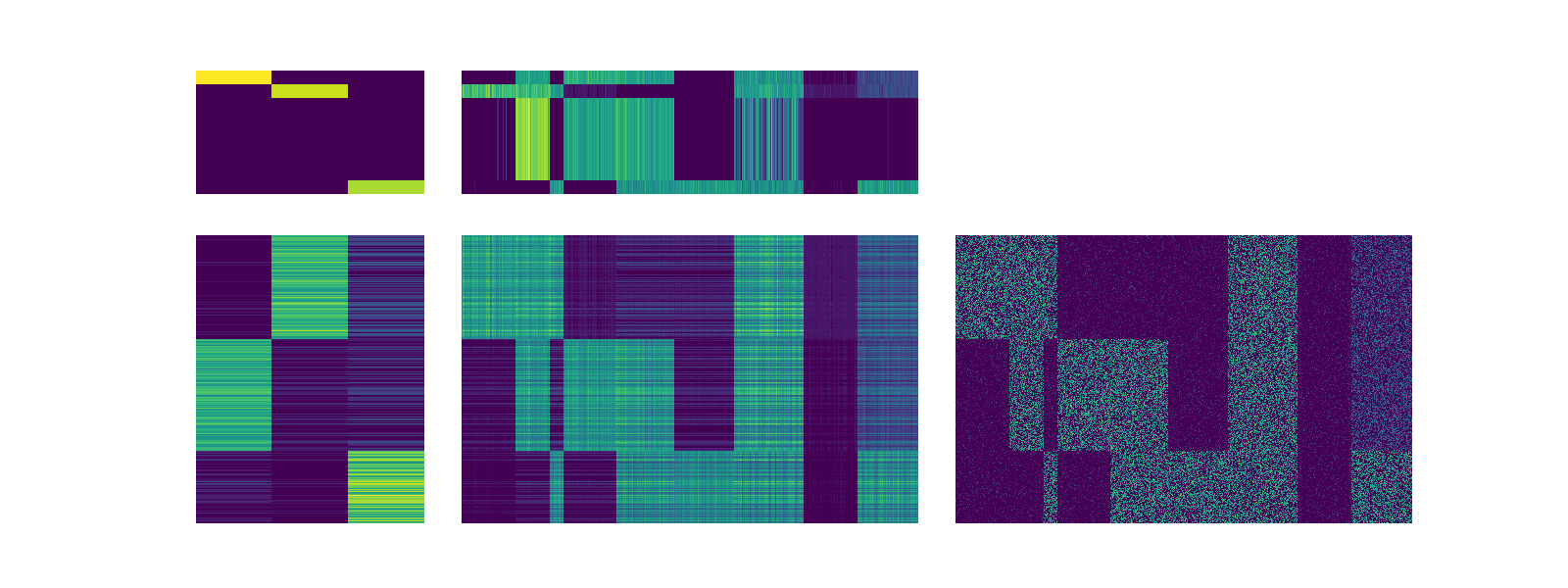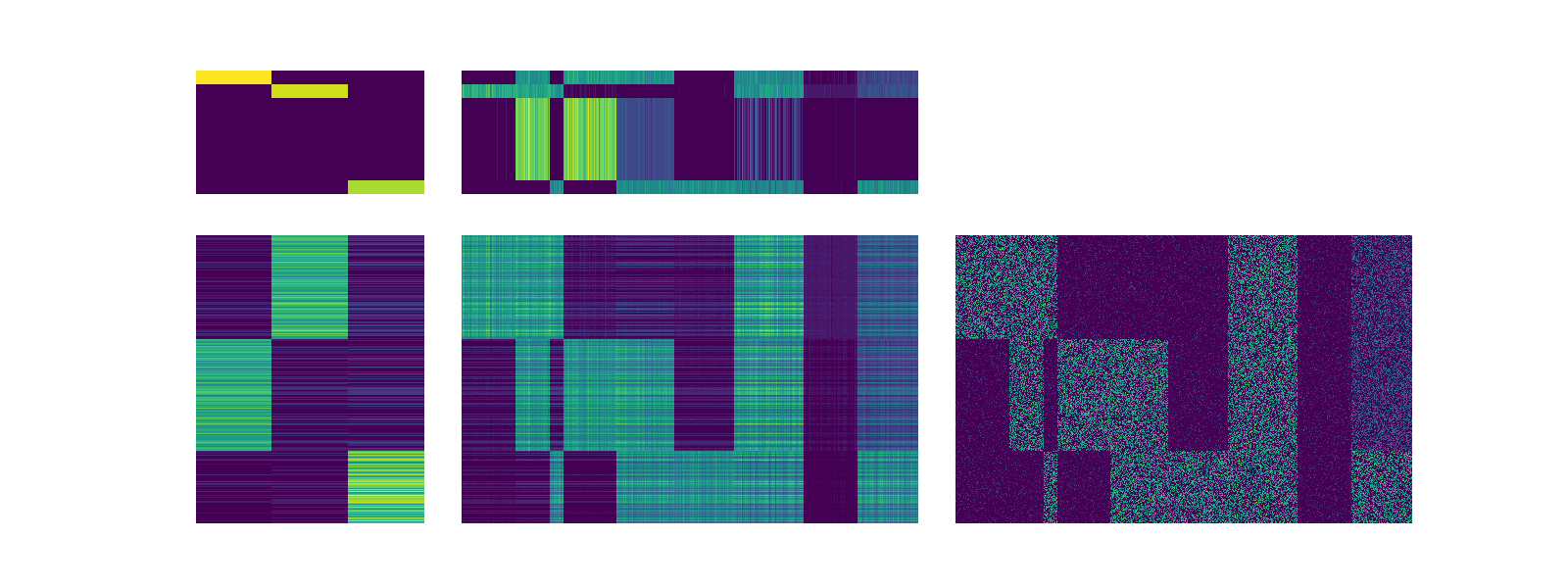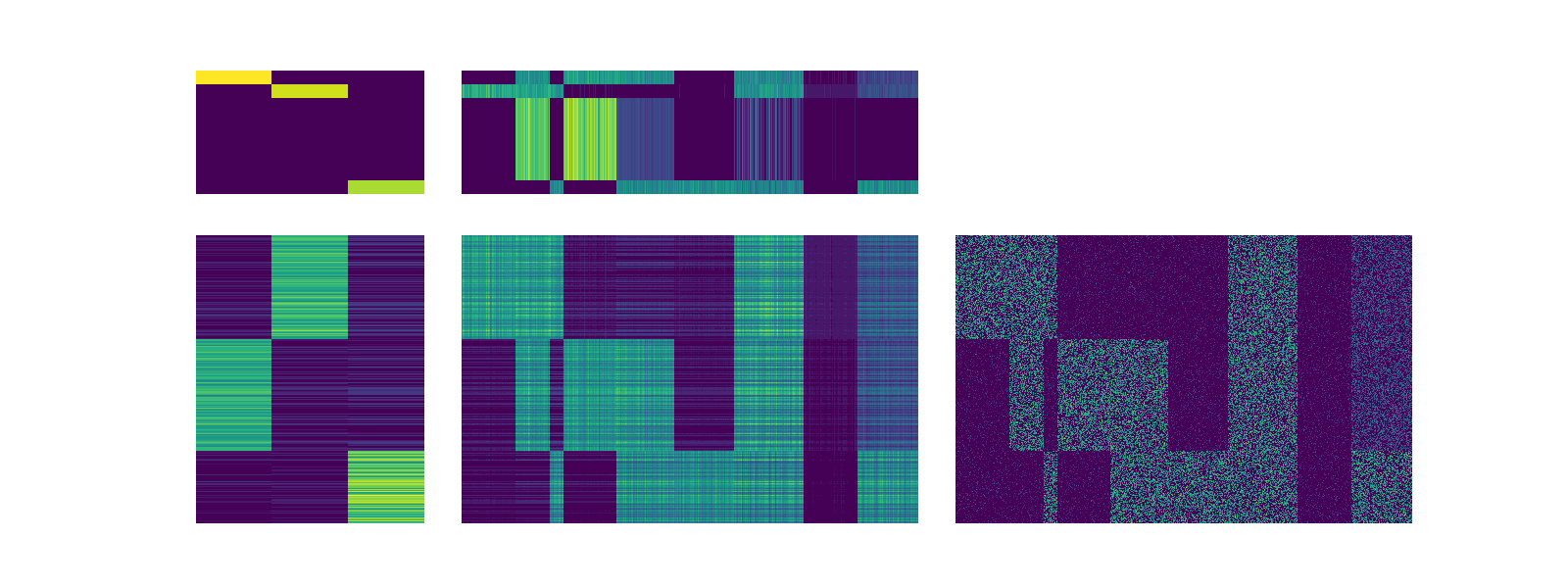
In this context, without regularization, the SCOTCH fit is roughly equivalent to the NMF fit. First the three U factors, are related to a single V factor (this is indicated by the three bright values of the S matrix). Each of the three main factors of V represent the mean profile of each of the correspond cell blocks. The remaining factors of V (3-8) are contributing little to the estimation scheme). Below we repeat the SCOTCH runs with regularization. The value of lambda can range from $[0, 1]$ but in practice we find that the values between $0.05$ and $0.20$ produce orthogonal vector representations of U and V without drastically increasing the reconstructions error.
scotch = SCOTCH.SCOTCH(k1 = 3, k2 = 9, max_l_u = 0.15, max_l_v = 0.15, term_tol = 1e-10, var_lambda= False, device = "cpu", init_style="random", max_iter=200)
scotch.draw_intermediate_graph = True
scotch.add_data_from_adata(adata)
scotch.fit()
Initializing NMTF factors Beginning NMTF Iter: 1 Iter Time: 0.108 Total Time: 0.108 Objective: 8.179e+06 Relative Delta Objective: 2.102e-01 Reconstruction Error: 8.179e+06 Iter: 2 Iter Time: 0.074 Total Time: 0.182 Objective: 7.971e+06 Relative Delta Objective: 2.539e-02 Reconstruction Error: 7.971e+06 Iter: 3 Iter Time: 0.046 Total Time: 0.228 Objective: 7.528e+06 Relative Delta Objective: 5.562e-02 Reconstruction Error: 7.528e+06 Iter: 4 Iter Time: 0.044 Total Time: 0.272 Objective: 7.331e+06 Relative Delta Objective: 2.615e-02 Reconstruction Error: 7.331e+06 Iter: 5 Iter Time: 0.045 Total Time: 0.316 Objective: 7.228e+06 Relative Delta Objective: 1.402e-02 Reconstruction Error: 7.228e+06 Iter: 6 Iter Time: 0.210 Total Time: 0.527 Objective: 7.122e+06 Relative Delta Objective: 1.468e-02 Reconstruction Error: 7.122e+06 Iter: 7 Iter Time: 0.044 Total Time: 0.571 Objective: 6.987e+06 Relative Delta Objective: 1.901e-02 Reconstruction Error: 6.987e+06 Iter: 8 Iter Time: 0.050 Total Time: 0.621 Objective: 6.889e+06 Relative Delta Objective: 1.402e-02 Reconstruction Error: 6.889e+06 Iter: 9 Iter Time: 0.053 Total Time: 0.674 Objective: 6.861e+06 Relative Delta Objective: 4.105e-03 Reconstruction Error: 6.861e+06 Iter: 10 Iter Time: 0.054 Total Time: 0.728 Objective: 6.855e+06 Relative Delta Objective: 7.902e-04 Reconstruction Error: 6.855e+06 Iter: 11 Iter Time: 0.062 Total Time: 0.790 Objective: 6.856e+06 Relative Delta Objective: -1.282e-04 Reconstruction Error: 6.856e+06 Iter: 12 Iter Time: 0.051 Total Time: 0.841 Objective: 6.858e+06 Relative Delta Objective: -2.930e-04 Reconstruction Error: 6.858e+06 Iter: 13 Iter Time: 0.050 Total Time: 0.891 Objective: 6.859e+06 Relative Delta Objective: -1.691e-04 Reconstruction Error: 6.859e+06 Iter: 14 Iter Time: 0.049 Total Time: 0.940 Objective: 6.860e+06 Relative Delta Objective: -6.014e-05 Reconstruction Error: 6.860e+06 Iter: 15 Iter Time: 0.048 Total Time: 0.988 Objective: 6.860e+06 Relative Delta Objective: -6.232e-05 Reconstruction Error: 6.860e+06 Iter: 16 Iter Time: 0.052 Total Time: 1.040 Objective: 6.861e+06 Relative Delta Objective: -1.389e-04 Reconstruction Error: 6.861e+06 Iter: 17 Iter Time: 0.042 Total Time: 1.082 Objective: 6.861e+06 Relative Delta Objective: -1.100e-05 Reconstruction Error: 6.861e+06 Iter: 18 Iter Time: 0.043 Total Time: 1.125 Objective: 6.861e+06 Relative Delta Objective: -1.377e-05 Reconstruction Error: 6.861e+06 Iter: 19 Iter Time: 0.051 Total Time: 1.176 Objective: 6.861e+06 Relative Delta Objective: 9.036e-06 Reconstruction Error: 6.861e+06 Iter: 20 Iter Time: 0.135 Total Time: 1.311 Objective: 6.861e+06 Relative Delta Objective: 5.750e-05 Reconstruction Error: 6.861e+06 Iter: 21 Iter Time: 0.040 Total Time: 1.351 Objective: 6.860e+06 Relative Delta Objective: 8.345e-05 Reconstruction Error: 6.860e+06 Iter: 22 Iter Time: 0.058 Total Time: 1.409 Objective: 6.859e+06 Relative Delta Objective: 1.003e-04 Reconstruction Error: 6.859e+06 Iter: 23 Iter Time: 0.056 Total Time: 1.465 Objective: 6.859e+06 Relative Delta Objective: 2.872e-05 Reconstruction Error: 6.859e+06 Iter: 24 Iter Time: 0.065 Total Time: 1.529 Objective: 6.859e+06 Relative Delta Objective: -3.572e-06 Reconstruction Error: 6.859e+06 Iter: 25 Iter Time: 0.059 Total Time: 1.589 Objective: 6.859e+06 Relative Delta Objective: -1.174e-05 Reconstruction Error: 6.859e+06 Iter: 26 Iter Time: 0.041 Total Time: 1.630 Objective: 6.859e+06 Relative Delta Objective: -2.435e-05 Reconstruction Error: 6.859e+06 Iter: 27 Iter Time: 0.043 Total Time: 1.673 Objective: 6.860e+06 Relative Delta Objective: -6.896e-05 Reconstruction Error: 6.860e+06 Iter: 28 Iter Time: 0.043 Total Time: 1.716 Objective: 6.860e+06 Relative Delta Objective: -7.471e-05 Reconstruction Error: 6.860e+06 Iter: 29 Iter Time: 0.053 Total Time: 1.769 Objective: 6.861e+06 Relative Delta Objective: -9.132e-05 Reconstruction Error: 6.861e+06 Iter: 30 Iter Time: 0.042 Total Time: 1.812 Objective: 6.862e+06 Relative Delta Objective: -7.572e-05 Reconstruction Error: 6.862e+06 Iter: 31 Iter Time: 0.039 Total Time: 1.851 Objective: 6.862e+06 Relative Delta Objective: -6.281e-05 Reconstruction Error: 6.862e+06 Iter: 32 Iter Time: 0.042 Total Time: 1.893 Objective: 6.862e+06 Relative Delta Objective: -5.326e-05 Reconstruction Error: 6.862e+06 Iter: 33 Iter Time: 0.043 Total Time: 1.936 Objective: 6.863e+06 Relative Delta Objective: -5.727e-05 Reconstruction Error: 6.863e+06 Iter: 34 Iter Time: 0.045 Total Time: 1.981 Objective: 6.863e+06 Relative Delta Objective: -3.096e-05 Reconstruction Error: 6.863e+06 Iter: 35 Iter Time: 0.045 Total Time: 2.026 Objective: 6.863e+06 Relative Delta Objective: -2.477e-06 Reconstruction Error: 6.863e+06 Iter: 36 Iter Time: 0.041 Total Time: 2.068 Objective: 6.863e+06 Relative Delta Objective: -3.278e-06 Reconstruction Error: 6.863e+06 Iter: 37 Iter Time: 0.143 Total Time: 2.211 Objective: 6.863e+06 Relative Delta Objective: 1.683e-05 Reconstruction Error: 6.863e+06 Iter: 38 Iter Time: 0.043 Total Time: 2.253 Objective: 6.863e+06 Relative Delta Objective: 3.825e-05 Reconstruction Error: 6.863e+06 Iter: 39 Iter Time: 0.043 Total Time: 2.296 Objective: 6.862e+06 Relative Delta Objective: 5.923e-05 Reconstruction Error: 6.862e+06 Iter: 40 Iter Time: 0.044 Total Time: 2.340 Objective: 6.862e+06 Relative Delta Objective: 4.794e-05 Reconstruction Error: 6.862e+06 Iter: 41 Iter Time: 0.043 Total Time: 2.383 Objective: 6.862e+06 Relative Delta Objective: 4.241e-05 Reconstruction Error: 6.862e+06 Iter: 42 Iter Time: 0.043 Total Time: 2.426 Objective: 6.862e+06 Relative Delta Objective: -3.133e-06 Reconstruction Error: 6.862e+06 Iter: 43 Iter Time: 0.061 Total Time: 2.486 Objective: 6.862e+06 Relative Delta Objective: -4.154e-05 Reconstruction Error: 6.862e+06 Iter: 44 Iter Time: 0.056 Total Time: 2.543 Objective: 6.862e+06 Relative Delta Objective: -6.062e-05 Reconstruction Error: 6.862e+06 Iter: 45 Iter Time: 0.056 Total Time: 2.599 Objective: 6.863e+06 Relative Delta Objective: -7.935e-05 Reconstruction Error: 6.863e+06 Iter: 46 Iter Time: 0.068 Total Time: 2.667 Objective: 6.863e+06 Relative Delta Objective: -7.045e-05 Reconstruction Error: 6.863e+06 Iter: 47 Iter Time: 0.056 Total Time: 2.723 Objective: 6.864e+06 Relative Delta Objective: -7.059e-05 Reconstruction Error: 6.864e+06 Iter: 48 Iter Time: 0.053 Total Time: 2.775 Objective: 6.864e+06 Relative Delta Objective: -4.910e-05 Reconstruction Error: 6.864e+06 Iter: 49 Iter Time: 0.061 Total Time: 2.837 Objective: 6.864e+06 Relative Delta Objective: -4.167e-05 Reconstruction Error: 6.864e+06 Iter: 50 Iter Time: 0.055 Total Time: 2.891 Objective: 6.865e+06 Relative Delta Objective: -2.739e-05 Reconstruction Error: 6.865e+06 Iter: 51 Iter Time: 0.056 Total Time: 2.948 Objective: 6.865e+06 Relative Delta Objective: -4.326e-05 Reconstruction Error: 6.865e+06 Iter: 52 Iter Time: 0.041 Total Time: 2.989 Objective: 6.865e+06 Relative Delta Objective: -3.853e-05 Reconstruction Error: 6.865e+06 Iter: 53 Iter Time: 0.047 Total Time: 3.035 Objective: 6.866e+06 Relative Delta Objective: -4.049e-05 Reconstruction Error: 6.866e+06 Iter: 54 Iter Time: 0.040 Total Time: 3.076 Objective: 6.866e+06 Relative Delta Objective: -4.311e-05 Reconstruction Error: 6.866e+06 Iter: 55 Iter Time: 0.050 Total Time: 3.126 Objective: 6.866e+06 Relative Delta Objective: -5.302e-05 Reconstruction Error: 6.866e+06 Iter: 56 Iter Time: 0.045 Total Time: 3.170 Objective: 6.867e+06 Relative Delta Objective: -5.229e-05 Reconstruction Error: 6.867e+06 Iter: 57 Iter Time: 0.042 Total Time: 3.212 Objective: 6.867e+06 Relative Delta Objective: -5.330e-05 Reconstruction Error: 6.867e+06 Iter: 58 Iter Time: 0.043 Total Time: 3.255 Objective: 6.867e+06 Relative Delta Objective: -5.410e-05 Reconstruction Error: 6.867e+06 Iter: 59 Iter Time: 0.167 Total Time: 3.422 Objective: 6.868e+06 Relative Delta Objective: -5.359e-05 Reconstruction Error: 6.868e+06 Iter: 60 Iter Time: 0.043 Total Time: 3.465 Objective: 6.868e+06 Relative Delta Objective: -4.740e-05 Reconstruction Error: 6.868e+06 Iter: 61 Iter Time: 0.041 Total Time: 3.506 Objective: 6.868e+06 Relative Delta Objective: -4.186e-05 Reconstruction Error: 6.868e+06 Iter: 62 Iter Time: 0.040 Total Time: 3.546 Objective: 6.869e+06 Relative Delta Objective: -3.756e-05 Reconstruction Error: 6.869e+06 Iter: 63 Iter Time: 0.042 Total Time: 3.588 Objective: 6.869e+06 Relative Delta Objective: -3.290e-05 Reconstruction Error: 6.869e+06 Iter: 64 Iter Time: 0.048 Total Time: 3.636 Objective: 6.869e+06 Relative Delta Objective: -2.977e-05 Reconstruction Error: 6.869e+06 Iter: 65 Iter Time: 0.042 Total Time: 3.678 Objective: 6.869e+06 Relative Delta Objective: -2.875e-05 Reconstruction Error: 6.869e+06 Iter: 66 Iter Time: 0.041 Total Time: 3.719 Objective: 6.869e+06 Relative Delta Objective: -2.744e-05 Reconstruction Error: 6.869e+06 Iter: 67 Iter Time: 0.041 Total Time: 3.760 Objective: 6.869e+06 Relative Delta Objective: -2.213e-05 Reconstruction Error: 6.869e+06 Iter: 68 Iter Time: 0.040 Total Time: 3.800 Objective: 6.870e+06 Relative Delta Objective: -1.885e-05 Reconstruction Error: 6.870e+06 Iter: 69 Iter Time: 0.042 Total Time: 3.842 Objective: 6.870e+06 Relative Delta Objective: -1.892e-05 Reconstruction Error: 6.870e+06 Iter: 70 Iter Time: 0.051 Total Time: 3.893 Objective: 6.870e+06 Relative Delta Objective: -1.885e-05 Reconstruction Error: 6.870e+06 Iter: 71 Iter Time: 0.042 Total Time: 3.935 Objective: 6.870e+06 Relative Delta Objective: -1.958e-05 Reconstruction Error: 6.870e+06 Iter: 72 Iter Time: 0.041 Total Time: 3.976 Objective: 6.870e+06 Relative Delta Objective: -1.870e-05 Reconstruction Error: 6.870e+06 Iter: 73 Iter Time: 0.042 Total Time: 4.017 Objective: 6.870e+06 Relative Delta Objective: -1.870e-05 Reconstruction Error: 6.870e+06 Iter: 74 Iter Time: 0.043 Total Time: 4.061 Objective: 6.870e+06 Relative Delta Objective: -1.718e-05 Reconstruction Error: 6.870e+06 Iter: 75 Iter Time: 0.047 Total Time: 4.108 Objective: 6.870e+06 Relative Delta Objective: -1.150e-05 Reconstruction Error: 6.870e+06 Iter: 76 Iter Time: 0.040 Total Time: 4.148 Objective: 6.871e+06 Relative Delta Objective: -7.496e-06 Reconstruction Error: 6.871e+06 Iter: 77 Iter Time: 0.049 Total Time: 4.197 Objective: 6.871e+06 Relative Delta Objective: 9.461e-07 Reconstruction Error: 6.871e+06 Iter: 78 Iter Time: 0.042 Total Time: 4.239 Objective: 6.870e+06 Relative Delta Objective: 6.477e-06 Reconstruction Error: 6.870e+06 Iter: 79 Iter Time: 0.043 Total Time: 4.282 Objective: 6.870e+06 Relative Delta Objective: 1.390e-05 Reconstruction Error: 6.870e+06 Iter: 80 Iter Time: 0.042 Total Time: 4.324 Objective: 6.870e+06 Relative Delta Objective: 2.016e-05 Reconstruction Error: 6.870e+06 Iter: 81 Iter Time: 0.042 Total Time: 4.367 Objective: 6.870e+06 Relative Delta Objective: 2.875e-05 Reconstruction Error: 6.870e+06 Iter: 82 Iter Time: 0.042 Total Time: 4.409 Objective: 6.870e+06 Relative Delta Objective: 4.309e-05 Reconstruction Error: 6.870e+06 Iter: 83 Iter Time: 0.047 Total Time: 4.456 Objective: 6.869e+06 Relative Delta Objective: 5.022e-05 Reconstruction Error: 6.869e+06 Iter: 84 Iter Time: 0.041 Total Time: 4.497 Objective: 6.869e+06 Relative Delta Objective: 6.456e-05 Reconstruction Error: 6.869e+06 Iter: 85 Iter Time: 0.045 Total Time: 4.542 Objective: 6.869e+06 Relative Delta Objective: 6.333e-05 Reconstruction Error: 6.869e+06 Iter: 86 Iter Time: 0.187 Total Time: 4.729 Objective: 6.868e+06 Relative Delta Objective: 6.173e-05 Reconstruction Error: 6.868e+06 Iter: 87 Iter Time: 0.049 Total Time: 4.778 Objective: 6.868e+06 Relative Delta Objective: 5.780e-05 Reconstruction Error: 6.868e+06 Iter: 88 Iter Time: 0.044 Total Time: 4.822 Objective: 6.867e+06 Relative Delta Objective: 4.849e-05 Reconstruction Error: 6.867e+06 Iter: 89 Iter Time: 0.042 Total Time: 4.864 Objective: 6.867e+06 Relative Delta Objective: 4.165e-05 Reconstruction Error: 6.867e+06 Iter: 90 Iter Time: 0.042 Total Time: 4.907 Objective: 6.867e+06 Relative Delta Objective: 3.357e-05 Reconstruction Error: 6.867e+06 Iter: 91 Iter Time: 0.041 Total Time: 4.948 Objective: 6.867e+06 Relative Delta Objective: 2.774e-05 Reconstruction Error: 6.867e+06 Iter: 92 Iter Time: 0.046 Total Time: 4.993 Objective: 6.867e+06 Relative Delta Objective: 2.184e-05 Reconstruction Error: 6.867e+06 Iter: 93 Iter Time: 0.044 Total Time: 5.037 Objective: 6.866e+06 Relative Delta Objective: 1.544e-05 Reconstruction Error: 6.866e+06 Iter: 94 Iter Time: 0.044 Total Time: 5.081 Objective: 6.866e+06 Relative Delta Objective: 1.085e-05 Reconstruction Error: 6.866e+06 Iter: 95 Iter Time: 0.044 Total Time: 5.125 Objective: 6.866e+06 Relative Delta Objective: 7.646e-06 Reconstruction Error: 6.866e+06 Iter: 96 Iter Time: 0.040 Total Time: 5.165 Objective: 6.866e+06 Relative Delta Objective: 5.898e-06 Reconstruction Error: 6.866e+06 Iter: 97 Iter Time: 0.044 Total Time: 5.209 Objective: 6.866e+06 Relative Delta Objective: 4.588e-06 Reconstruction Error: 6.866e+06 Iter: 98 Iter Time: 0.042 Total Time: 5.252 Objective: 6.866e+06 Relative Delta Objective: 3.423e-06 Reconstruction Error: 6.866e+06 Iter: 99 Iter Time: 0.044 Total Time: 5.295 Objective: 6.866e+06 Relative Delta Objective: 2.330e-06 Reconstruction Error: 6.866e+06 Iter: 100 Iter Time: 0.043 Total Time: 5.339 Objective: 6.866e+06 Relative Delta Objective: 2.622e-06 Reconstruction Error: 6.866e+06 Iter: 101 Iter Time: 0.040 Total Time: 5.378 Objective: 6.866e+06 Relative Delta Objective: 2.112e-06 Reconstruction Error: 6.866e+06 Iter: 102 Iter Time: 0.046 Total Time: 5.425 Objective: 6.866e+06 Relative Delta Objective: 1.748e-06 Reconstruction Error: 6.866e+06 Iter: 103 Iter Time: 0.052 Total Time: 5.477 Objective: 6.866e+06 Relative Delta Objective: 1.238e-06 Reconstruction Error: 6.866e+06 Iter: 104 Iter Time: 0.040 Total Time: 5.517 Objective: 6.866e+06 Relative Delta Objective: 8.739e-07 Reconstruction Error: 6.866e+06 Iter: 105 Iter Time: 0.042 Total Time: 5.559 Objective: 6.866e+06 Relative Delta Objective: 4.369e-07 Reconstruction Error: 6.866e+06 Iter: 106 Iter Time: 0.042 Total Time: 5.600 Objective: 6.866e+06 Relative Delta Objective: 2.913e-07 Reconstruction Error: 6.866e+06 Iter: 107 Iter Time: 0.043 Total Time: 5.643 Objective: 6.866e+06 Relative Delta Objective: 1.456e-07 Reconstruction Error: 6.866e+06 Iter: 108 Iter Time: 0.047 Total Time: 5.690 Objective: 6.866e+06 Relative Delta Objective: 7.282e-08 Reconstruction Error: 6.866e+06 Iter: 109 Iter Time: 0.042 Total Time: 5.732 Objective: 6.866e+06 Relative Delta Objective: 0.000e+00 Reconstruction Error: 6.866e+06
scotch.write_gif('NMTF_lU_lV_0.15.gif')
writing gif to ./NMTF_lU_lV_0.15.gif
This factorization produces a much richer representation in S which indicate the relationship between column clusters and row clusters. The function below plots the factors in a manor where they are sorted by the U and V with maximum contributions. In the sorted representation below we can see that most factors of U and V are orthogonal. Notably, some of the factors in V, e.g. 3, 4, and 5, larely reflect a similar trend in the matrix. Specifically, they capture columns which are representation in all clusters.
fig = scotch.visualize_factors_sorted()
display(fig)
The orthogonal representation naturally lends itself to assigning these row and column features to clusters. For each row of U and V (note the representation above shows $V^T$) we assign them to the cluster based on the $argmax(U[i, :])$ and $argmax(V[i, :])$. The clustering is implemented in the assign_cluster function below. After assigning clusters, the SCOTCH information can be directly added back to the adata object using he addScotchEmbeddingToAnnData() function.
scotch.assign_cluster()
scotch.add_scotch_embeddings_to_adata(adata, 'NMTF_lU_lV_0.15')
AnnData object with n_obs × n_vars = 500 × 1000
obs: 'NMTF_lU_lV_0.15_cell_clusters'
var: 'NMTF_lU_lV_0.15_gene_clusters'
uns: 'NMTF_lU_lV_0.15_S_matrix', 'NMTF_lU_lV_0.15_reconstruction_error', 'NMTF_lU_lV_0.15_error'
obsm: 'NMTF_lU_lV_0.15_cell_embedding', 'NMTF_lU_lV_0.15_P_embedding'
varm: 'NMTF_lU_lV_0.15_gene_embedding', 'NMTF_lU_lV_0.15_Q_embedding'
We can visualize the different U and V components using UMAP below. The first UMAP is generated using PCA. The second and third UMAP are generated using the SCOTCH embeddings. First using $U$, and second using $U*S = P$. The $U$ matrix's orthogonality may lead to poor representations in the UMAP space due to the instability in the knn graph. Generally this can be improved by increasing the number of neighbors. The $P$ embedding generally produces better representation in the UMAP space because it is less effected by the orthogonality constraint. The 4th UMAP demonstrates the relationships captured in the column space.
sc.pp.pca(adata)
sc.pp.neighbors(adata, use_rep= "X_pca")
sc.tl.umap(adata)
sc.pl.umap(adata, color = "NMTF_lU_lV_0.15_cell_clusters")
sc.pp.pca(adata)
sc.pp.neighbors(adata, use_rep= "NMTF_lU_lV_0.15_cell_embedding", n_neighbors= 100)
sc.tl.umap(adata)
sc.pl.umap(adata, color = "NMTF_lU_lV_0.15_cell_clusters")
sc.pp.pca(adata)
sc.pp.neighbors(adata, use_rep= "NMTF_lU_lV_0.15_P_embedding", n_neighbors= 100)
sc.tl.umap(adata)
sc.pl.umap(adata, color = "NMTF_lU_lV_0.15_cell_clusters")
adata_genes = adata.T
sc.pp.pca(adata_genes)
sc.pp.neighbors(adata_genes, use_rep= "NMTF_lU_lV_0.15_Q_embedding", n_neighbors= 300)
sc.tl.umap(adata_genes)
sc.pl.umap(adata_genes, color = "NMTF_lU_lV_0.15_gene_clusters")
/opt/anaconda3/envs/Pytorch/lib/python3.9/site-packages/sklearn/manifold/_spectral_embedding.py:274: UserWarning: Graph is not fully connected, spectral embedding may not work as expected. warnings.warn(
SCOTCH provides cluster visualization technique where the clusters are ordered, and each alternating cluster is assigned either a black or grey barcode.
scotch.visualize_clusters()
scotch.visualize_clusters_sorted()
The scotch update is susceptible to poor initialization which results in multiple factors representation similar contributions in V. This can result in some of the errors in clustering. One method to get around this is to utilize NMTF to generate a lower embedding, clustering the embedding, and using this as an initialization which accurately capture the relationship between factors. This is performed using the reclusterV function below.
scotch.recluster_V()
scotch.assign_cluster()
Iter: 1 Iter Time: 0.243 Total Time: 0.243 Objective: 6.858e+06 Relative Delta Objective: 7.597e-04 Reconstruction Error: 6.858e+06 Iter: 2 Iter Time: 0.061 Total Time: 0.304 Objective: 6.858e+06 Relative Delta Objective: -6.657e-05 Reconstruction Error: 6.858e+06 Iter: 3 Iter Time: 0.057 Total Time: 0.360 Objective: 6.859e+06 Relative Delta Objective: -1.027e-04 Reconstruction Error: 6.859e+06 Iter: 4 Iter Time: 0.047 Total Time: 0.407 Objective: 6.859e+06 Relative Delta Objective: -5.154e-05 Reconstruction Error: 6.859e+06 Iter: 5 Iter Time: 0.059 Total Time: 0.466 Objective: 6.859e+06 Relative Delta Objective: -3.601e-05 Reconstruction Error: 6.859e+06 Iter: 6 Iter Time: 0.069 Total Time: 0.535 Objective: 6.860e+06 Relative Delta Objective: -3.550e-05 Reconstruction Error: 6.860e+06 Iter: 7 Iter Time: 0.069 Total Time: 0.604 Objective: 6.860e+06 Relative Delta Objective: -4.162e-05 Reconstruction Error: 6.860e+06 Iter: 8 Iter Time: 0.073 Total Time: 0.676 Objective: 6.860e+06 Relative Delta Objective: -4.942e-05 Reconstruction Error: 6.860e+06 Iter: 9 Iter Time: 0.072 Total Time: 0.749 Objective: 6.861e+06 Relative Delta Objective: -6.049e-05 Reconstruction Error: 6.861e+06 Iter: 10 Iter Time: 0.060 Total Time: 0.809 Objective: 6.861e+06 Relative Delta Objective: -6.770e-05 Reconstruction Error: 6.861e+06 Iter: 11 Iter Time: 0.089 Total Time: 0.897 Objective: 6.862e+06 Relative Delta Objective: -6.457e-05 Reconstruction Error: 6.862e+06 Iter: 12 Iter Time: 0.057 Total Time: 0.955 Objective: 6.862e+06 Relative Delta Objective: -5.560e-05 Reconstruction Error: 6.862e+06 Iter: 13 Iter Time: 0.052 Total Time: 1.006 Objective: 6.862e+06 Relative Delta Objective: -4.037e-05 Reconstruction Error: 6.862e+06 Iter: 14 Iter Time: 0.045 Total Time: 1.051 Objective: 6.863e+06 Relative Delta Objective: -2.485e-05 Reconstruction Error: 6.863e+06 Iter: 15 Iter Time: 0.073 Total Time: 1.124 Objective: 6.863e+06 Relative Delta Objective: -8.015e-06 Reconstruction Error: 6.863e+06 Iter: 16 Iter Time: 0.047 Total Time: 1.171 Objective: 6.862e+06 Relative Delta Objective: 1.209e-05 Reconstruction Error: 6.862e+06 Iter: 17 Iter Time: 0.169 Total Time: 1.340 Objective: 6.862e+06 Relative Delta Objective: 4.736e-06 Reconstruction Error: 6.862e+06 Iter: 18 Iter Time: 0.050 Total Time: 1.390 Objective: 6.862e+06 Relative Delta Objective: 2.689e-05 Reconstruction Error: 6.862e+06 Iter: 19 Iter Time: 0.043 Total Time: 1.433 Objective: 6.862e+06 Relative Delta Objective: 2.324e-05 Reconstruction Error: 6.862e+06 Iter: 20 Iter Time: 0.042 Total Time: 1.475 Objective: 6.862e+06 Relative Delta Objective: 3.629e-05 Reconstruction Error: 6.862e+06 Iter: 21 Iter Time: 0.046 Total Time: 1.521 Objective: 6.862e+06 Relative Delta Objective: 2.784e-05 Reconstruction Error: 6.862e+06 Iter: 22 Iter Time: 0.055 Total Time: 1.577 Objective: 6.861e+06 Relative Delta Objective: 2.536e-05 Reconstruction Error: 6.861e+06 Iter: 23 Iter Time: 0.046 Total Time: 1.623 Objective: 6.861e+06 Relative Delta Objective: 1.137e-05 Reconstruction Error: 6.861e+06 Iter: 24 Iter Time: 0.050 Total Time: 1.673 Objective: 6.861e+06 Relative Delta Objective: 1.385e-06 Reconstruction Error: 6.861e+06 Iter: 25 Iter Time: 0.049 Total Time: 1.722 Objective: 6.861e+06 Relative Delta Objective: -6.558e-07 Reconstruction Error: 6.861e+06 Iter: 26 Iter Time: 0.049 Total Time: 1.771 Objective: 6.861e+06 Relative Delta Objective: 1.166e-06 Reconstruction Error: 6.861e+06 Iter: 27 Iter Time: 0.057 Total Time: 1.828 Objective: 6.861e+06 Relative Delta Objective: 3.352e-06 Reconstruction Error: 6.861e+06 Iter: 28 Iter Time: 0.044 Total Time: 1.872 Objective: 6.861e+06 Relative Delta Objective: 5.538e-06 Reconstruction Error: 6.861e+06 Iter: 29 Iter Time: 0.045 Total Time: 1.917 Objective: 6.861e+06 Relative Delta Objective: 3.279e-06 Reconstruction Error: 6.861e+06 Iter: 30 Iter Time: 0.064 Total Time: 1.981 Objective: 6.861e+06 Relative Delta Objective: 3.206e-06 Reconstruction Error: 6.861e+06 Iter: 31 Iter Time: 0.055 Total Time: 2.035 Objective: 6.861e+06 Relative Delta Objective: 2.478e-06 Reconstruction Error: 6.861e+06 Iter: 32 Iter Time: 0.062 Total Time: 2.098 Objective: 6.861e+06 Relative Delta Objective: 4.810e-06 Reconstruction Error: 6.861e+06 Iter: 33 Iter Time: 0.049 Total Time: 2.146 Objective: 6.861e+06 Relative Delta Objective: 3.644e-06 Reconstruction Error: 6.861e+06 Iter: 34 Iter Time: 0.047 Total Time: 2.194 Objective: 6.861e+06 Relative Delta Objective: 2.915e-06 Reconstruction Error: 6.861e+06 Iter: 35 Iter Time: 0.065 Total Time: 2.259 Objective: 6.861e+06 Relative Delta Objective: 5.538e-06 Reconstruction Error: 6.861e+06 Iter: 36 Iter Time: 0.057 Total Time: 2.316 Objective: 6.861e+06 Relative Delta Objective: 3.935e-06 Reconstruction Error: 6.861e+06 Iter: 37 Iter Time: 0.069 Total Time: 2.385 Objective: 6.861e+06 Relative Delta Objective: 2.623e-06 Reconstruction Error: 6.861e+06 Iter: 38 Iter Time: 0.180 Total Time: 2.565 Objective: 6.861e+06 Relative Delta Objective: 6.340e-06 Reconstruction Error: 6.861e+06 Iter: 39 Iter Time: 0.047 Total Time: 2.611 Objective: 6.861e+06 Relative Delta Objective: 5.101e-06 Reconstruction Error: 6.861e+06 Iter: 40 Iter Time: 0.045 Total Time: 2.656 Objective: 6.861e+06 Relative Delta Objective: 4.883e-06 Reconstruction Error: 6.861e+06 Iter: 41 Iter Time: 0.042 Total Time: 2.698 Objective: 6.861e+06 Relative Delta Objective: 1.822e-06 Reconstruction Error: 6.861e+06 Iter: 42 Iter Time: 0.051 Total Time: 2.750 Objective: 6.861e+06 Relative Delta Objective: 3.571e-06 Reconstruction Error: 6.861e+06 Iter: 43 Iter Time: 0.056 Total Time: 2.806 Objective: 6.861e+06 Relative Delta Objective: 2.478e-06 Reconstruction Error: 6.861e+06 Iter: 44 Iter Time: 0.052 Total Time: 2.858 Objective: 6.861e+06 Relative Delta Objective: 1.822e-06 Reconstruction Error: 6.861e+06 Iter: 45 Iter Time: 0.046 Total Time: 2.904 Objective: 6.861e+06 Relative Delta Objective: 1.530e-06 Reconstruction Error: 6.861e+06 Iter: 46 Iter Time: 0.043 Total Time: 2.947 Objective: 6.861e+06 Relative Delta Objective: 1.312e-06 Reconstruction Error: 6.861e+06 Iter: 47 Iter Time: 0.054 Total Time: 3.000 Objective: 6.861e+06 Relative Delta Objective: 1.166e-06 Reconstruction Error: 6.861e+06 Iter: 48 Iter Time: 0.057 Total Time: 3.058 Objective: 6.861e+06 Relative Delta Objective: 1.020e-06 Reconstruction Error: 6.861e+06 Iter: 49 Iter Time: 0.049 Total Time: 3.106 Objective: 6.861e+06 Relative Delta Objective: 1.020e-06 Reconstruction Error: 6.861e+06 Iter: 50 Iter Time: 0.045 Total Time: 3.151 Objective: 6.861e+06 Relative Delta Objective: 8.745e-07 Reconstruction Error: 6.861e+06 Iter: 51 Iter Time: 0.052 Total Time: 3.203 Objective: 6.861e+06 Relative Delta Objective: 3.134e-06 Reconstruction Error: 6.861e+06 Iter: 52 Iter Time: 0.044 Total Time: 3.246 Objective: 6.861e+06 Relative Delta Objective: 1.239e-06 Reconstruction Error: 6.861e+06 Iter: 53 Iter Time: 0.052 Total Time: 3.298 Objective: 6.861e+06 Relative Delta Objective: -2.186e-07 Reconstruction Error: 6.861e+06 Iter: 54 Iter Time: 0.046 Total Time: 3.344 Objective: 6.861e+06 Relative Delta Objective: 2.186e-07 Reconstruction Error: 6.861e+06 Iter: 55 Iter Time: 0.041 Total Time: 3.386 Objective: 6.861e+06 Relative Delta Objective: 2.915e-07 Reconstruction Error: 6.861e+06 Iter: 56 Iter Time: 0.048 Total Time: 3.433 Objective: 6.861e+06 Relative Delta Objective: 2.915e-07 Reconstruction Error: 6.861e+06 Iter: 57 Iter Time: 0.062 Total Time: 3.495 Objective: 6.861e+06 Relative Delta Objective: 2.186e-07 Reconstruction Error: 6.861e+06 Iter: 58 Iter Time: 0.065 Total Time: 3.560 Objective: 6.861e+06 Relative Delta Objective: 1.458e-07 Reconstruction Error: 6.861e+06 Iter: 59 Iter Time: 0.059 Total Time: 3.619 Objective: 6.861e+06 Relative Delta Objective: 1.458e-07 Reconstruction Error: 6.861e+06 Iter: 60 Iter Time: 0.054 Total Time: 3.673 Objective: 6.861e+06 Relative Delta Objective: 7.288e-08 Reconstruction Error: 6.861e+06 Iter: 61 Iter Time: 0.064 Total Time: 3.737 Objective: 6.861e+06 Relative Delta Objective: 7.288e-08 Reconstruction Error: 6.861e+06 Iter: 62 Iter Time: 0.050 Total Time: 3.787 Objective: 6.861e+06 Relative Delta Objective: 0.000e+00 Reconstruction Error: 6.861e+06
scotch.visualize_factors()
After running this function the elements of better capture different natural column clusters.
scotch.visualize_clusters()
scotch.visualize_clusters_sorted()